DETERMINAN
MATRIKS
Determinan matriks A didefinisikan sebagai selisih antara perkalian elemen-elemen pada diagonal utama dengan perkalian elemen-elemen pada diagonal sekunder. Determinan dari matriks A dinotasikan dengan det A atau |A|.
Determinan matriks A didefinisikan sebagai selisih antara perkalian elemen-elemen pada diagonal utama dengan perkalian elemen-elemen pada diagonal sekunder. Determinan dari matriks A dinotasikan dengan det A atau |A|.
Nilai dari
determinan suatu matriks berupa bilangan real.
a.
Determinan matriks berordo dua
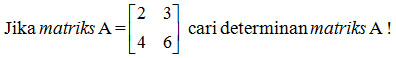
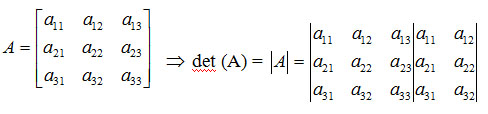
Det A=[A]=
a11 . a12 . a33 + a12 . a23 . a31 + a13 . a21 . a32 – a31 . a22 . a13 – a32 . a23 . a11 – a33 . a21 . a12
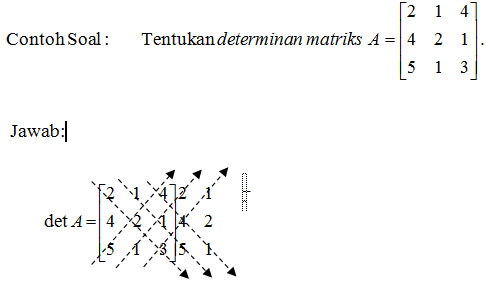
det A = 2.2.3 + 1.1.5 + 4.4.1 - 5.2.4 - 1.1.2 - 3.4.1
= 12 + 5 + 16 – 40 – 2 – 12
= -21
2. Adjoint Matriks
Adjoint yaitu koofaktor yangh di transposekan dan ditulis dengan Adj (A). Adjoin disingkat
Adj.
Adjoint suatu matriks bujur sangkar adalah :
Tidak ada komentar:
Posting Komentar